13. Volume

c1. Volume using Thin Disks

We first consider the problem of computing the volume of a solid of revolution using thin disks.

The region below a positive function \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b\) is rotated about the \(x\)-axis. Find the volume of the solid swept out.

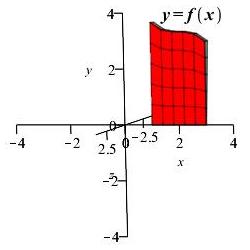
The plot shows a region under y = f of x above the x axis to be revolved.

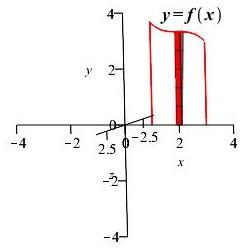
Since \(y\) is a function of \(x\), we will do an \(x\) integral. So we chop up the \(x\)-interval into small pieces of length \(\Delta x\). For the small interval located at \(x_i\), the corresponding small piece of the region is a rectangle and the corresponding small piece of the volume is a thin disk.

The thickness of each disk is \(\Delta x\) and the radius of the disk at \(x_i\) is \(r=f(x_i)\). So the area of the disk is: \[ A=\pi r^2=\pi f(x_i)^2 \] and its volume is: \[ \Delta V=A\,\Delta x=\pi f(x_i)^2\Delta x \] Adding up the volumes of the disks and taking the limit as the number of disks gets large (\(n\rightarrow \infty\)) and the thickness of each disk gets small (\(\Delta x\rightarrow 0\)) we obtain the volume of the solid of revolution: \[\begin{aligned} V&=\lim_{n\rightarrow\infty}\sum_{i=1}^n\Delta V =\lim_{n\rightarrow\infty}\sum_{i=1}^n\pi f(x_i)^2\Delta x \\ &=\int_a^b \pi\,f(x)^2\,dx \end{aligned}\]

The plot shows a vertical rectangle under y = f of x to be revolved.

Show Hand

Now turn your head sideways: A small happy face shows you to tilt your head to the right.

The region to the left of a positive function \(x=f(y)\) and to the right of the \(y\)-axis between \(y=a\) and \(y=b\) is rotated about the \(y\)-axis. Find the volume of the solid swept out.

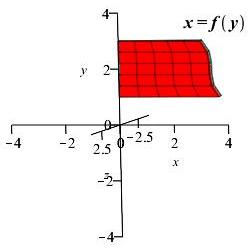
The plot shows a region between x = f of y and the y axis to be revolved.

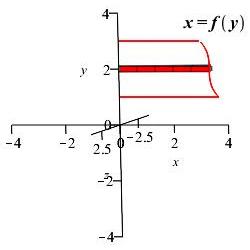
This time we chop up the \(y\)-interval into small pieces of length \(\Delta y\). Then the rectangles and disks are horizontal.

The volume of a disk is \(\Delta V=\pi f(y)^2\Delta y\) and the volume of the solid of revolution is: \[ V=\int_a^b \pi\,f(y)^2\,dy \]

The plot shows a horizontal rectangle between x = f of y and the y axis
to be revolved.

Show Hand

If the region below a positive function \(y=f(x)\) above the \(x\)-axis between \(x=a\) and \(x=b\) is rotated about the \(x\)-axis, the volume swept out is: \[ V=\int_a^b \pi f(x)^2\,dx \] If the region to the left of a positive function \(x=f(y)\) and to the right of the \(y\)-axis between \(y=a\) and \(y=b\) is rotated about the \(y\)-axis, the volume swept out is: \[ V=\int_a^b \pi f(y)^2\,dy \] Both formulas can be summarized as \[ V=\int_a^b \pi(\text{radius})^2\,dv \] where \(dv\) is either \(dx\) or \(dy\).

Notice that finding the volume of a solid of revolution by disks is really a special case of finding a volume by slicing \[ V=\int_a^b A(v)\,dv \] in which each cross-sectional area is the area of a circle, \(A=\pi(\text{radius})^2\).

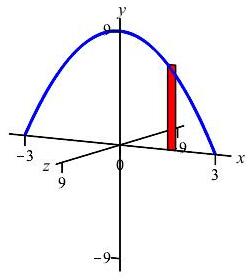
The region below the parabola \(y=9-x^2\) above the \(x\)-axis is rotated about the \(x\)-axis. Find the volume swept out.

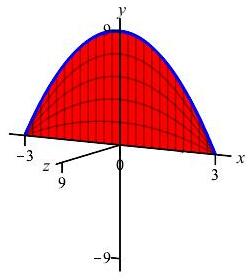
The plot shows the region below a parabola with x intercepts -3 and 3
and y intercept 9, to be revolved. — The Curve

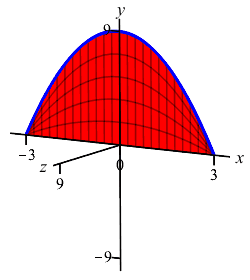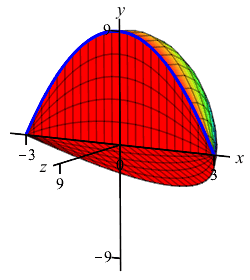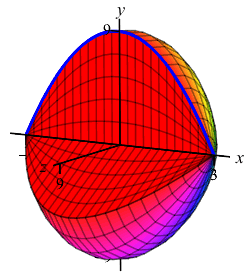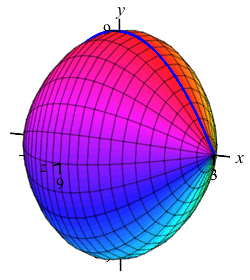
The animation shows the parabola rotating
about the x axis, forming a solid something like a football. — The Solid

We cut up the \(x\)-axis (because the curve is a function of \(x\), not because we rotate about the \(x\)-axis) and see that the rectangles are vertical and they rotate into thin disks:

The plot shows a vertical rectangle under the parabola, to be rotated. — A Riemann Rectangle

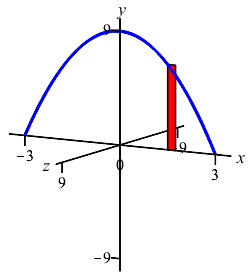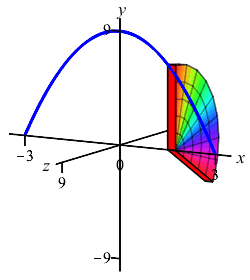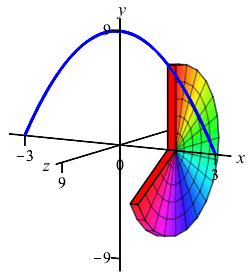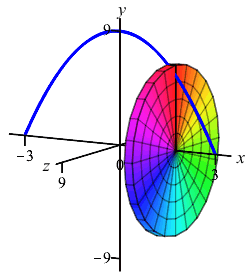
The animation shows the vertical rectangle rotating about
the x axis, forming a disk. — A Rectangle Rotates into a Disk

So the volume is \[\begin{aligned} V&=\int_a^b \pi f(x)^2\,dx =\int_{-3}^3 \pi(9-x^2)^2\,dx \\ &=\pi\int_{-3}^3 (81-18x^2+x^4)\,dx \\ &=\pi\left[81x-6x^3+\dfrac{x^5}{5}\right]_{-3}^3 =\dfrac{1296}{5}\pi \end{aligned}\]

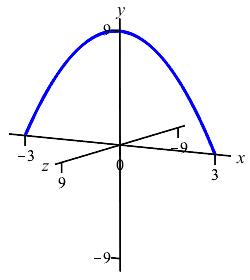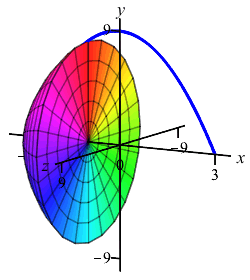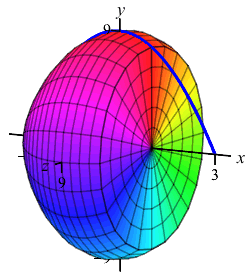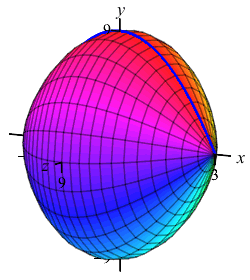
The animation shows the disks acumulating to form the football. — Accumulating Disks

Here are some more examples:

Example 1

Example 2

Now you try:

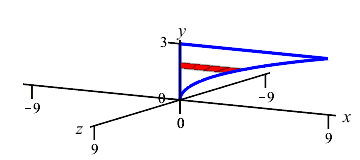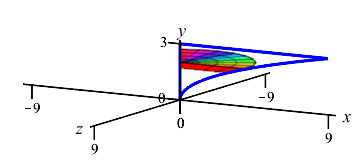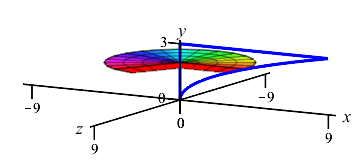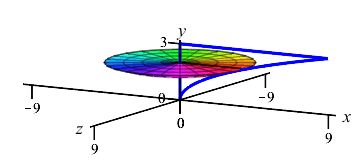
The region between \(x=y^2\) and the \(y\)-axis for \(0 \le y \le 3\) is rotated about the \(y\)-axis. Find the volume swept out.

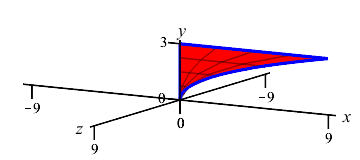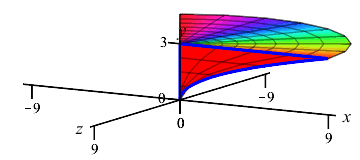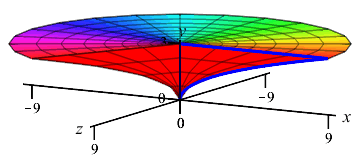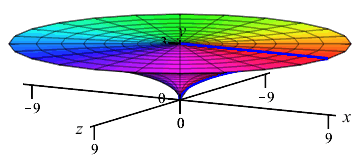
This shows the area between a parabola opening right and the line
y equals 3, swept around the y-axis.

The curve is a function of \(y\); so this is a \(y\)-integral and we cut up the \(y\)-axis. Here is the region and one rotated disk:

This shows a slice of the area rotated around the y axis,
forming a disk.

\(\displaystyle V=\dfrac{243\pi}{5}\)

The curve is a function of \(y\); so this is a \(y\)-integral and we cut up the \(y\)-axis. Here is the region and one rotated disk:

The radius of the disk is \(r=x=y^2\). So the area is \(A=\pi r^2=\pi y^4\) and the volume is \[ V=\int_0^3 \pi y^4\,dy =\left[\pi\dfrac{y^5}{5}\right]_0^3 =\dfrac{243\pi}{5} \]

13. Volume

c1. Volume using Thin Disks

Heading